TYS-RBAモデル Index
Wiki管理
合同会社TYS
技術開発部
TEL 042-812-5920
水理水文ソフトウェア
GIS関連のソフトウェア
Fortranで水理計算
Javaで水理計算
Excelで水文水理計算
TYSのHP
— mail to TYS Support
複断面は、レベル2の平均流公式を用いることで、分割断面ごとにそれぞれ水深(水位は一定)・流速を求めることができるため、それぞれの流砂量を求めることができる。しかしながら、レベル1の平均流公式を用いた台形断面が混在する場合には、各分割断面のエネルギー勾配や、上流からの流砂量の振り分け等取り扱いに無理がある部分があり、明らかに1次元の計算の範疇を越えてしまう。したがって、各分割断面を1つにまとめた形で流砂量計算を行うものとする。具体的には、複断面の流積:、径深:(井田の合成径深)として、断面緒元を1つにまとめて取り扱う。
また、水位が高水敷よりも上にある場でも、高水敷内に移動可能な土砂が存在しない場合(=計算河床が高水敷よりも下にある)には、高水敷の幅を考慮に入れないこととする。つまり、移動可能な土砂が存在する幅に対する流砂量で河床変動を議論することとする。
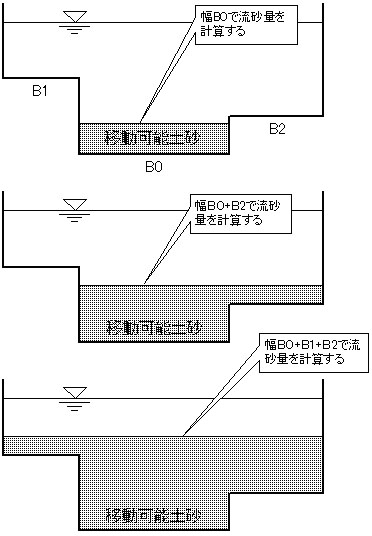
図-4.1 複断面の河床高に応じた流砂量の取り扱い
エネルギー勾配の大小は、そのまま当該断面の流砂量に大きく影響するため、計算結果に異常洗掘・異常堆積が見られる場合、水面形の扱いもしくはエネルギー勾配の扱いをチェックする必要がある。 エネルギー勾配の取り方は、
・・・(4.1)
ここで、:上流のエネルギー、:下流のエネルギーで、各エネルギーは位置エネルギーと運動エネルギーの和で表される。
・・・(4.2)
しかし、上式の場合、位置エネルギーの差がほとんどないような地形=前後の河床勾配が小さな地形では、運動エネルギーの差がそのままエネルギー勾配に反映されることとなり、地形形状の急変部等では常に洗掘傾向にある箇所と堆積傾向にある箇所が極端になるような不安定な状況が起こることがある。(具体的な状態として、計算後の河床が波打ったように凹凸を繰り返す状況) よって、断面間のエネルギー損失よりエネルギー勾配を求める式として以下の式を用いる。
・・・(4.3)
(4.3)式は河床変動計算を説明した論文や書籍にしばしば見られる記述(例えば、「山地河川における河床変動の数値計算法(社)砂防学会編」:発行山海堂、p15」)であり、厳密には矩形の断面形状が一様な区間で用いるべき方法である。
これら二つの方法を地形条件等に応じて使い分ける必要があるが、TYS-RBAモデルでは(4.3)式を用いて計算している。
「土石流の機構と対策(高橋 保)」P341より、急勾配河床において、渓床堆積物により河床が階段状を呈している場合、ある程度水深が大きくなるまでは、局所的な水面勾配が平均的な地形勾配よりも小さくなると考えられる。この時、流砂量は、抑制されると考えられる。本モデルでは、その効果を前節で求めたエネルギー勾配に補正係数を乗ずる形式で表現する。エネルギー勾配の補正係数:rは
・・・(4.4)
で求める。ここで、:水深、:90%粒径、ただし、r<1.0である。
つまり、90%粒径よりも浅いような流量の小さな状況では、階段状河床形態を考慮してエネルギー勾配を補正するということである。
ダム地点のエネルギー勾配の取り扱いは、計算条件に応じて結果が異なるため、これはという決め手がないのが現状であるが、おおよその傾向をまとめると以下の通りになる。
一般断面で(4.1)式の考え方を用いた場合、ダム断面と1つ下流の断面では、ダムの堤体の存在により水面形は不連続になっているため、そのまま(4.1)式を用いることはできない。
そのため、
等の方法が用いられる。一方、一般断面で(4.3)式を用いる場合、ダム地点においても、そのまま(4.3)式を利用する。
また、ダム地点の流砂量の取り扱いについては、不透過ダム・スリットダムで取り扱いが異なっている。詳細については、3-7・3-8を参照のこと。